Simple Interpolation

---

This is the first of a multiple part series I'm doing on interpolation and spline functions. This post focuses on the simplest interpolation functions, which provide a smooth transition between (only) two values. I'll provide generic C++ source code at the end of the series.

An interpolation function defines how a variable changes between two values (e.g. starting and ending position of an object) with respect to a third value (e.g. time). A spline allows smooth interpolation between an arbitrary number of control points, by defining a separate function for the interval between each control point. Splines are also very useful for drawing curves. Splines will be discussed in detail in the next post.

This post is going to focus on interpolating between two values. These simple interpolation functions can help polish any changing variable. Objects with changing position, rotation, scale, skew, color, or opacity can benefit from a smooth transition defined by simple interpolation.

The most basic interpolation function is the step function. It just jumps from one value to the next halfway through.

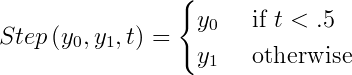
Nobody really uses the Step function on purpose. Instead, it shows up accidentally everywhere an unpolished transition is made. Whenever a programmer instantly repositions an object on the screen, he accidentally used the step function. If a game character gets hit, and his health bar display instantly updates, the Step function strikes again.

The simplest real interpolation function is Linear interpolation, also known as Lerp. It transitions from one value to another at a constant rate, using a straightforward and intuitive formula. The downside is its infinite acceleration and deceleration. When Linear interpolation is used to control movement or rotational speed, it has a tendency to look jerky. Still, it's a huge leap better than the Step function.

Smooth Interpolation

So we need to modify the Linear function to provide a smooth acceleration and deceleration. An obvious way of doing this is to scale t using a smooth function. Cosine is a suitably smooth function.

We only need to take the first half period, so our Cosine based interpolation function looks like:

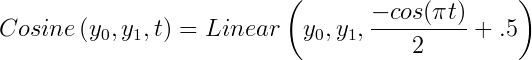
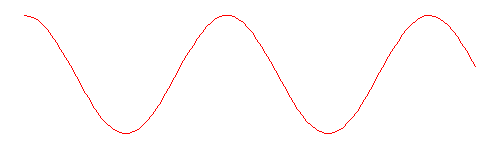
You can see Linear and Cosine interpolation compared in the animation below. The triangle on the left has a jerky start and end, while the Cosine interpolated rotation on the right has a smooth start and end.

A nearly identical polynomial function can also be constructed. It is called SmoothStep. In some applications it may be more efficient than calculating Cosine.

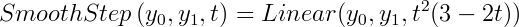
Either Cosine or SmoothStep interpolation can replace almost all Linear interpolation for a smoother, more polished result.

I'd like to note just two more interpolation functions: Acceleration and Deceleration.

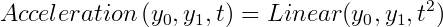
These functions are mainly useful for moving objects into or out of view. Acceleration can be useful for moving an object smoothly off the screen, because it has a sharp stop, but smooth start.

Visualizations

Here are three more comparisons: color interpolation, position interpolation, and a graph of the discussed functions.

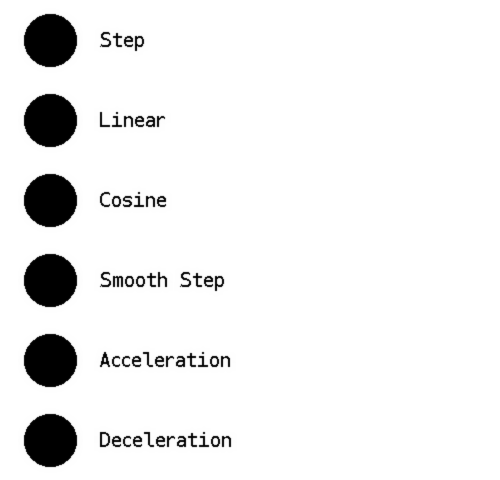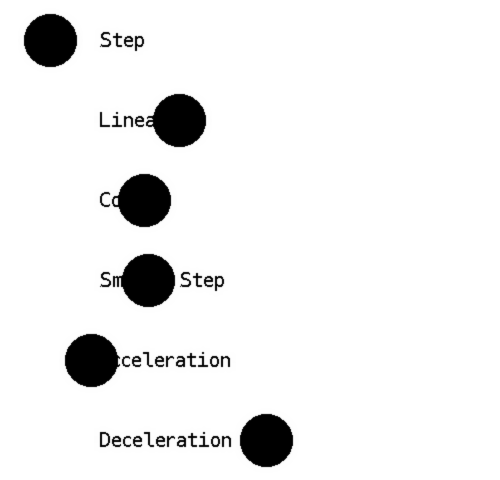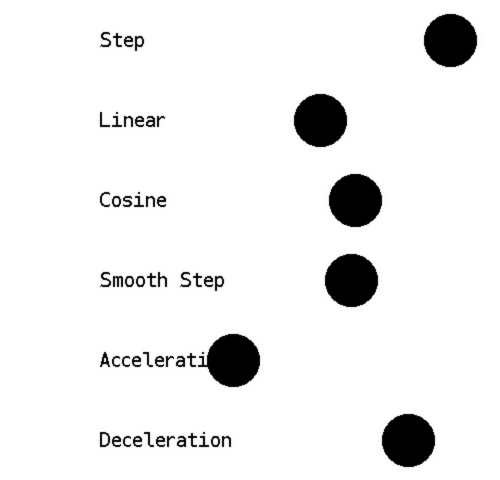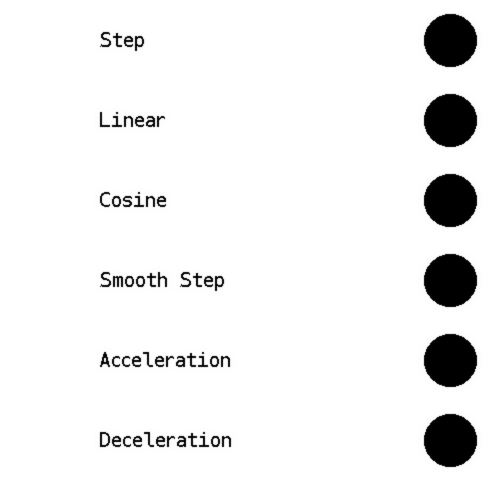
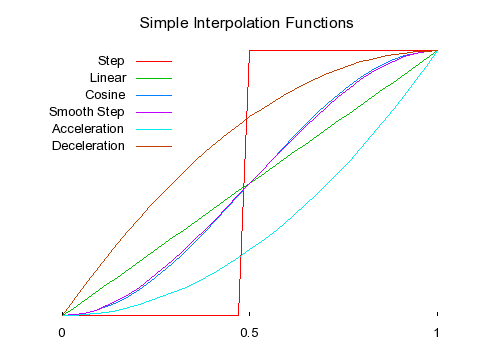
In the next post, interpolation functions will be combined over several points to create splines.

---

---